Month: October 2024

Statistics can often be a daunting field, filled with complex formulas and intricate concepts. One such concept is the “standard error formula,” which plays a crucial role in statistical analysis. Whether you’re a student, researcher, or data enthusiast, grasping the standard error formula is essential for accurate data interpretation.

Key Takeaways

• The standard error formula is fundamental in statistics, providing a measure of the accuracy of a sample mean compared to the population mean.
• It helps in estimating the variability and reliability of data, crucial for hypothesis testing and constructing confidence intervals.
• Understanding the standard error is vital for interpreting statistical results and making informed decisions based on data.

What is the Standard Error?

The standard error (SE) is a statistical term that reflects the variability of a sample statistic, most commonly the mean, from the true population mean. It provides insight into how much the sample mean would vary if different samples were taken from the same population. The smaller the standard error, the more representative the sample mean is of the population mean.

The Importance of the Standard Error

The standard error is crucial for several reasons:

• Precision of Estimates: A smaller standard error indicates more precise estimates of the population parameter.
• Confidence Intervals: SE is used to construct confidence intervals, which indicate the range within which the true population parameter is likely to fall.
• Hypothesis Testing: It plays a role in hypothesis testing, helping to determine if observed data is statistically significant.

Calculating the Standard Error Formula

The standard error formula varies depending on the statistic being estimated. For the sample mean, the formula is:

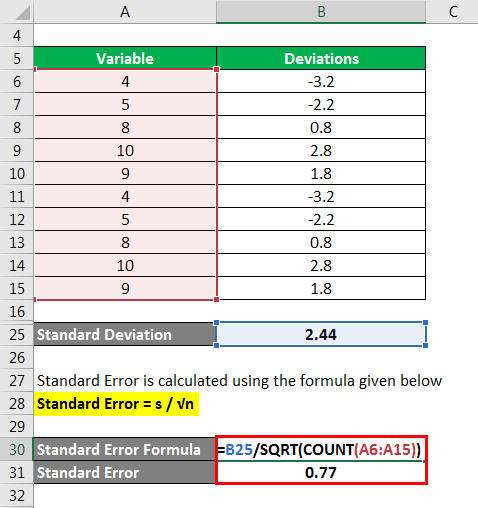
SE = s / √n

Where:

• s is the sample standard deviation.
• n is the sample size.

Steps to Calculate the Standard Error

1. Calculate the sample mean (average of your data).
2. Determine the sample standard deviation.
3. Divide the sample standard deviation by the square root of the sample size.

Applications of the Standard Error Formula

The standard error formula is applied in various statistical analyses, including:

1. Constructing Confidence Intervals

Confidence intervals provide a range of values that likely contain the population parameter. The standard error is used to determine the margin of error in these intervals, influencing their width and reliability.

2. Hypothesis Testing

In hypothesis testing, the standard error helps determine the test statistic, which is used to decide whether to reject or fail to reject the null hypothesis. A smaller SE indicates more reliable test results.

3. Regression Analysis

In regression analysis, the standard error of the estimate measures the accuracy of predictions. It helps in assessing how well the regression line fits the data.

Factors Affecting the Standard Error

Several factors can influence the magnitude of the standard error:

1. Sample Size

A larger sample size generally results in a smaller standard error, as it provides more information about the population, leading to more accurate estimates.

2. Variability in Data

High variability within a dataset increases the standard error. More consistent data will result in a lower SE, indicating more reliable estimates.

3. Sampling Method

The method used to select samples can affect the standard error. Random sampling tends to yield more accurate estimates compared to non-random sampling methods.

Interpreting the Standard Error

Understanding the implications of the standard error is crucial for data analysis:

1. Small Standard Error

A small standard error suggests that the sample mean is a reliable estimate of the population mean, indicating low variability among sample means.

2. Large Standard Error

A large standard error indicates greater variability among sample means, suggesting that the sample mean may not be a precise estimate of the population mean.

The standard error formula is an essential tool in the realm of statistics, offering insights into the accuracy and reliability of sample estimates. By understanding and applying the standard error, researchers and analysts can make informed decisions based on statistical data. Whether you’re constructing confidence intervals, conducting hypothesis tests, or performing regression analysis, the standard error plays a pivotal role in ensuring the validity and reliability of your findings.

Mastering the standard error formula will enhance your ability to interpret statistical results accurately, ultimately leading to more robust conclusions and better decision-making based on data.

Key Takeaways

• An in-depth look at Rowan Francis Henchy, focusing on his life, influence, and achievements.
• Understanding the background and family connections of Rowan Francis Henchy.
• Insightful details about his personal and professional life.
• Comprehensive analysis of his impact on popular culture.

In the world of entertainment and celebrity culture, certain names resonate with a unique charm and allure. One such name is Rowan Francis Henchy. This article delves into the intriguing life of Rowan Francis Henchy, examining his background, family, and the impact he has had on popular culture. By the end of this piece, you will have a well-rounded understanding of who Rowan Francis Henchy is and why he is a name to remember.

Who is Rowan Francis Henchy?

Rowan Francis Henchy is a name that has been gaining attention in various circles, primarily due to his famous lineage and the potential he holds for the future. Born into a family that is no stranger to the spotlight, Rowan is the son of actress Brooke Shields and television writer and producer Chris Henchy. This unique combination of talent and creativity has undoubtedly paved the way for Rowan’s potential future endeavors in the entertainment industry.

The Family Background

The Henchy family is a fascinating blend of artistic and creative prowess. Brooke Shields, Rowan’s mother, is a celebrated actress and model known for her roles in films such as “The Blue Lagoon” and “Endless Love.” Her presence in Hollywood has been significant, and she continues to be a prominent figure in the entertainment industry.

Chris Henchy, Rowan’s father, is a successful television writer and producer. He is best known for his work on popular shows such as “Entourage” and “The Other Guys.” His contributions to television and film have earned him a reputation as a talented and innovative creator.

The Early Life of Rowan Francis Henchy

Rowan Francis Henchy was born on May 15, 2003, in Los Angeles, California. From a young age, Rowan was exposed to the glitz and glamour of Hollywood, thanks to his parents’ successful careers. Despite this, his upbringing was grounded and focused on providing him with a well-rounded education and a sense of normalcy.

Rowan’s parents have always emphasized the importance of education and personal growth. As a result, he has been encouraged to pursue his interests and passions, whether they lie in the arts, academics, or sports. This balanced approach has allowed Rowan to develop a strong sense of self and a clear vision for his future.

Rowan’s Interests and Hobbies

Like many teenagers, Rowan Francis Henchy has a diverse range of interests and hobbies. He is known to be passionate about sports, particularly basketball, and often participates in local games and tournaments. This love for sports not only keeps him physically active but also instills a sense of teamwork and discipline.

In addition to sports, Rowan has shown an interest in the arts, much like his parents. Whether it’s exploring music, acting, or writing, Rowan’s creative pursuits are encouraged and nurtured by his family. This support system has allowed him to explore various avenues and discover his true passions.

Rowan Francis Henchy’s Influence on Popular Culture

While Rowan Francis Henchy is still a young individual, his potential impact on popular culture is significant. Being the offspring of two influential figures in the entertainment industry, Rowan has the unique opportunity to carve out his own niche and make a name for himself.

As he continues to grow and develop his skills, Rowan’s influence is expected to expand. Whether he chooses to follow in his parents’ footsteps or forge his own path, the world will undoubtedly be watching his journey with great interest.

The Future of Rowan Francis Henchy

As Rowan Francis Henchy transitions from adolescence to adulthood, the world eagerly anticipates what the future holds for him. With a strong foundation provided by his family and a wealth of opportunities at his disposal, Rowan is well-equipped to make a significant impact in whatever field he chooses to pursue.

Whether he becomes a prominent figure in the entertainment industry, an advocate for social causes, or a leader in another field, Rowan’s journey will be one to watch. His unique background and upbringing have prepared him for success, and his potential is limitless.

Rowan Francis Henchy is a name that carries with it a sense of promise and potential. As the son of Brooke Shields and Chris Henchy, Rowan has been exposed to the world of entertainment from a young age, and his future is undoubtedly bright. With a strong support system and a diverse range of interests, Rowan is poised to make a significant impact on popular culture and beyond.

As we continue to follow his journey, it is clear that Rowan Francis Henchy is a name that will be remembered for years to come. Whether he chooses to follow in his parents’ footsteps or blaze his own trail, the world is eager to see what he will achieve. The legacy of Rowan Francis Henchy is just beginning, and it promises to be an exciting and inspiring story.

Overalls for women have made a remarkable comeback in the fashion world, blending style, comfort, and versatility. Whether you’re aiming for a casual look or something more chic, overalls offer endless possibilities. In this guide, we will explore everything you need to know about overalls for women, from style tips to choosing the perfect fit.

Key Takeaways

• Overalls for women are versatile and can be styled for various occasions.
• They come in different materials, including denim, cotton, and linen.
• Accessorizing overalls can elevate your look from casual to sophisticated.
• Understanding fit and body type is crucial for selecting the right overalls.

Why Overalls for Women Are a Fashion Staple

Overalls have transcended their origins as workwear to become a fashion staple for women. Their appeal lies in their adaptability and comfort. Unlike traditional jeans or skirts, overalls offer a unique silhouette that can be dressed up or down, making them suitable for a variety of settings.

The Evolution of Overalls

Originally designed for laborers in the 18th century, overalls were created for durability and functionality. Fast forward to the present day, and overalls have evolved into a trendy piece of clothing that combines practicality with style. Designers have embraced overalls, offering them in a range of fabrics, colors, and cuts.

Choosing the Right Material

When selecting overalls for women, the material plays a significant role in both comfort and style. Here are some popular options:

• Denim: The classic choice, denim overalls are durable and versatile. They can be paired with a simple t-shirt for a casual look or dressed up with a blouse and heels.
• Cotton: Lightweight and breathable, cotton overalls are ideal for warmer weather. They offer a relaxed fit and are perfect for a laid-back style.
• Linen: Known for its cooling properties, linen overalls are great for summer. They provide an elegant and airy feel, perfect for beach outings or casual brunches.

Styling Tips for Overalls

One of the best things about overalls for women is their versatility. Here are some styling tips to help you make the most of your overalls:

Casual Day Out

For a relaxed daytime look, pair your denim overalls with a graphic tee and sneakers. Add a baseball cap and a backpack for an effortlessly cool vibe.

Office Ready

Transform your overalls into office-appropriate attire by choosing a tailored pair in a neutral color. Layer with a crisp white shirt and add loafers or ankle boots to complete the look.

Evening Elegance

For a night out, opt for black or dark-colored overalls. Pair them with a silk blouse and statement jewelry. Complete the ensemble with strappy heels and a clutch bag for a chic appearance.

Accessorizing Your Overalls

Accessories can significantly enhance the look of overalls for women. Consider these options:

• Belt: Adding a belt can define your waist and add structure to your outfit.
• Jewelry: Statement necklaces or earrings can add a touch of elegance.
• Scarves: A colorful scarf can add a pop of color and personality to your look.
• Bags: Choose a handbag or backpack that complements the color and style of your overalls.

Finding the Perfect Fit

The key to rocking overalls is finding the right fit for your body type. Here are some tips to consider:

• Petite: Opt for slim-fit overalls to avoid overwhelming your frame. Cropped lengths can also elongate your legs.
• Curvy: Look for overalls with adjustable straps and a bit of stretch for added comfort. A-line cuts can flatter your shape.
• Tall: Choose overalls with longer inseams or adjustable hems to ensure a comfortable fit.

Caring for Your Overalls

To keep your overalls looking their best, follow these care tips:

• Always check the care label for specific washing instructions.
• Turn denim overalls inside out before washing to preserve color.
• Avoid using bleach on colored or patterned overalls to prevent fading.
• Hang or lay flat to dry to maintain the shape and integrity of the fabric.

Overalls for women are more than just a fashion trend; they are a versatile wardrobe essential that can be styled in numerous ways. By understanding the different materials, styling tips, and how to accessorize, you can create looks that are both comfortable and stylish. Remember to consider your body type when selecting overalls to ensure the perfect fit. With the right care, your overalls will remain a beloved part of your wardrobe for years to come.

Breastfeeding is a beautiful journey, but it can come with its set of challenges. One common issue that many nursing mothers face is a clogged milk duct. Understanding what it is, how to identify it, and how to treat it can make a significant difference in your breastfeeding experience. This article delves into all you need to know about clogged milk ducts, providing practical solutions and insights.

Key Takeaways

• A clogged milk duct is a common issue among breastfeeding mothers, characterized by a blockage in the milk flow.
• Symptoms include a tender lump in the breast, localized pain, and sometimes redness or warmth.
• Effective treatments include frequent breastfeeding, warm compresses, and gentle massage.
• Prevention strategies include proper breastfeeding techniques and ensuring complete breast drainage.

What is a Clogged Milk Duct?

A clogged milk duct occurs when a milk duct in the breast becomes blocked or restricted, preventing the milk from flowing freely. This can lead to a buildup of milk behind the blockage, causing discomfort and potential complications if not addressed promptly. Clogged ducts are most common during the early weeks of breastfeeding but can occur anytime during lactation.

Causes of Clogged Milk Ducts

Several factors can contribute to the development of a clogged milk duct. Understanding these causes can help in both prevention and treatment:

• Infrequent Nursing: Skipping feedings or not nursing frequently can lead to milk stasis, increasing the risk of blockages.
• Poor Latch: If the baby is not latching correctly, it can prevent efficient milk removal, leading to blockages.
• Pressure on the Breasts: Tight clothing or pressure from sleeping positions can restrict milk flow.
• Stress and Fatigue: High-stress levels and exhaustion can affect milk supply and flow.
• Overproduction of Milk: Producing more milk than the baby consumes can result in leftover milk, causing blockages.

Symptoms of a Clogged Milk Duct

Recognizing the signs of a clogged milk duct early can help in addressing the issue before it escalates. Common symptoms include:

• Tender Lump: A noticeable lump in the breast that feels tender to the touch.
• Localized Pain: Pain in a specific area of the breast, often accompanied by swelling.
• Redness and Warmth: The skin over the blocked duct may appear red and feel warm.
• Decreased Milk Supply: A noticeable drop in milk output from the affected breast.

Effective Solutions for Clogged Milk Ducts

Treating a clogged milk duct promptly is crucial to prevent it from developing into mastitis, a more serious breast infection. Here are some effective solutions:

Frequent Breastfeeding

One of the most effective ways to clear a clogged duct is to continue breastfeeding frequently. The baby’s sucking can help dislodge the blockage and promote milk flow. Ensure the baby is positioned correctly, and try different breastfeeding positions to facilitate drainage.

Warm Compresses

Applying a warm compress to the affected area can help in loosening the blockage. Use a warm, damp cloth or take a warm shower before breastfeeding to stimulate milk flow. The warmth can also provide relief from pain and swelling.

Gentle Massage

Massage the breast gently towards the nipple while nursing or pumping. This can help in breaking up the blockage and encouraging milk flow. Be careful not to apply too much pressure, as it can cause further irritation.

Proper Rest and Hydration

Ensure you are getting enough rest and staying hydrated. Fatigue and dehydration can affect milk production and flow. Taking care of your overall health can aid in faster recovery from a clogged duct.

Consulting a Lactation Expert

If the blockage persists or if you’re experiencing severe pain and fever, it may be time to consult a lactation consultant or healthcare provider. They can offer personalized advice and ensure there are no underlying issues.

Preventing Clogged Milk Ducts

While clogged milk ducts can be a common occurrence, certain strategies can help in minimizing the risk:

Ensure Proper Latch

A correct latch is crucial for effective milk removal. Make sure your baby is latching well and consider seeking guidance from a lactation consultant if you’re facing difficulties.

Regular Breastfeeding Schedule

Try to maintain a regular breastfeeding schedule to ensure consistent milk flow. Avoid skipping feedings and offer both breasts during each feeding session.

Avoid Pressure on Breasts

Wear comfortable, non-restrictive clothing and avoid sleeping positions that put pressure on your breasts. This can help in preventing blockages caused by external pressure.

Monitor Milk Supply

If you have an oversupply of milk, consider expressing milk after feedings to prevent blockages. However, be cautious not to overstimulate milk production.

Clogged milk ducts can be an uncomfortable experience for breastfeeding mothers, but with the right knowledge and strategies, they can be effectively managed and prevented. By understanding the causes and symptoms, and implementing effective solutions, you can ensure a smoother breastfeeding journey. Remember, if you’re ever in doubt or experiencing persistent issues, seeking professional guidance is always a wise choice.

Airbnb merupakan wadah di internet yang memungkinkan orang guna menyewakan properti mereka bagi tamu siapa menelusuri lokasi menginap guna periode pendek. Laman web ini memungkinkan individu guna meraih penghasilan suplemen dengan menyewakan kamar ataupun properti mereka bagi wisatawan asal semua dunia. Airbnb telah berubah keliru satu media terutama dikenal bagi akomodasi wisata internal sedikit tahun penutup.

Bagaimana Airbnb Bekerja

Proses menggunakan Airbnb sangat mudah. Pertama, individu siapa hendak menyewakan properti orang-orang itu harus mendaftar dan menciptakan profil dalam laman jaringan Airbnb. Selepas tersebut, mereka semua wajib menciptakan tabel properti mereka dengan foto-foto apa menggaet dan uraian apa detail. Calon tamu bisa melihat list properti apa tersedia serta memesan lokasi menetap mereka menggunakan website situs atau aplikasi Airbnb.

Ketika tamu memesan area bermukim melalui Airbnb, pemilik properti akan mendapat notifikasi dan juga mampu menerima atau menolak pesanan itu. Bila pesanan diterima, tamu dan juga pemilik properti mampu berhubungan melalui feature pesan di dalam website jaringan Airbnb bagi mengatur rincian kedatangan dan data lain-lain.

Keuntungan Menggunakan Airbnb

Ada berlimpah manfaat internal menggunakan Airbnb, bagus untuk pemilik properti either tamu. Untuk pemilik properti, Airbnb mengizinkan mereka semua guna meraih penghasilan ekstra asal properti orang-orang itu. Mereka Semua serta dapat menjangkau basis tamu siapa lebih besar melimpah dibandingkan dengan apabila mereka sekedar menyewakan properti orang-orang itu dengan wakil real estat kuno.

Sementara yang itu, kepada tamu, Airbnb memberikan bermacam-macam opsi akomodasi apa bermacam-macam, bermula asal kamar pribadi hingga segala rumah atau apartemen. Harga properti apa diberikan dari Airbnb juga dapat lebih terjangkau daripada hotel atau apartemen sewaan kuno.

Penyediaan Properti Guna Airbnb

Untuk berubah tuan rumah di Airbnb, pemilik properti perlu mempersiapkan properti orang-orang itu dengan bagus. Perkara ini mencakup membersihkan dan merapikan properti sebelumnya kedatangan tamu, memberikan perlengkapan mandi dan juga dapur, beserta mengomunikasikan aturan-aturan rumah bagi tamu serta terang.

Pemilik properti pula butuh menjamin bahwasanya list properti mereka di Airbnb menggaet dan juga informatif. Foto-foto properti siapa nyata dan juga deskripsi apa akurat bisa membantu menarik fokus calon tamu dan menaikkan probabilitas properti yang dimaksud disewakan.

Keamanan dan juga Perlindungan dalam Airbnb

Salah satu kekhawatiran pokok ketika memakai Airbnb adalah kendala keselamatan dan perlindungan. Namun, Airbnb pernah menyita bermacam-macam gerakan guna menyatakan keselamatan tamu serta pemilik properti. Feature verifikasi user dan rangkaian review bisa menolong menemukan user apa tidak cukup mampu dipercaya.

Selain yang itu, Airbnb juga menawarkan program perlindungan tamu serta tuan rumah guna menghadiahkan perlindungan internal kasus-kasus spesifik, sama seperti kerusakan properti ataupun perilaku siapa nggak pantas. Pemilik properti dan juga tamu pula bisa mendiskusikan persyaratan dan keperluan khusus mereka sebelum memesan sehingga kedua belah parti mengalami lebih banyak betah.

Apa yang Harus Dicermati Ketika Memakai Airbnb

Meskipun Airbnb memberikan banyak keuntungan kepada pemilik properti dan juga tamu, ada sejumlah perkara siapa perlu diperiksa ketika memanfaatkan platform ini. Mula-Mula, pastikanlah bagi mengecek ketentuan serta aturan Airbnb serta regulasi peraturan terkait penyewaan properti di dalam wilayah yang dimaksud.

Kedua, pastikanlah guna berbicara serta baik serta pemilik properti atau tamu sebelumnya kedatangan atau pemesanan. Masalah yang satu ini dapat membantu mencegah kebingungan ataupun kendala sewaktu proses penyewaan properti.

Terakhir, pastikanlah guna menghadiahkan tinjauan apa jujur dan juga akurat sesudah pengetahuan memanfaatkan Airbnb. Perkara ini bisa memudahkan manusia lain apa mencari area tinggal melalui media yang no. 1 ini dan mendirikan iman dalam di antara user Airbnb.

Kesimpulan

Airbnb merupakan media apa sekali terkenal bagi menyewakan properti untuk jangka pendek. Bersama persiapan siapa baik dan juga berbicara bersama bagus bersama pemilik properti atau tamu, kejadian memakai Airbnb dapat menjadi sangat mengasyikkan. Pastikan guna menyadari aturan serta kebijakan Airbnb serta memberikan ulasan siapa jujur dan tepat sesudah pengalaman Anda menggunakan media yang no. 1 ini.

Pembahasan mengenai Indonesia dan juga Libya sering menarik konsentrasi melimpah kelompok, bagus sebab segi historis, politis, either ekonomis. Second wilayah ini mempunyai latar belakang belakang serta jalur pembangunan yang tidak sama, siapa atas gilirannya menyusun kondisi sosial dan juga ekonomi orang-orang itu sama seperti sekarang yang no. 1 ini. Dalam karangan ini, kita semua akan menggali lebih besar di dalam tentang bagaimana dua bangsa ini, Indonesia dan Libya, berkomparasi satu seperti lainnya internal aspek ekonomi serta politik.

Sejarah Pendek Indonesia dan Libya

Indonesia, dengan melalui geografis terdapat dalam Asia Tenggara, adalah wilayah kepulauan terbesar pada dunia yang punya lebih banyak dari 17.000 island. Wilayah ini mendapatkan kemerdekaannya sebab Belanda di tahun 1945, dipelopori dari Soekarno dan juga Mohammad Hatta. Sejak tersebut, Indonesia sudah mengalami aneka pergolakan politik termasuk pemberontakan, pergantian presiden, serta zaman reformasi siapa pada akhirnya mengirim pada mekanisme demokrasi siapa lebih banyak stabil.

Sementara tersebut, Libya berada di wilayah Afrika Utara, berbatasan bersama Laut Mediterania. Libya merdeka sebab Italia atas tahun 1951 dan dikenal serta penguasaannya apa dahulu di bagian bawah kolonel Muammar Gaddafi siapa memerintah sejak tahun 1969 hingga 2011. Pasca kematian Gaddafi, Libya menderita ketidakstabilan politik dan juga konflik internal siapa berkepanjangan.

Aspek Politik: Pertimbangan Pemerintahan

Indonesia

Indonesia waktu ini merupakan republik presidensial, pada lokasi Presiden ialah pemimpin negara sekaligus pemerintahan. Bangsa yang nomor satu ini punya lebih besar dari 260 juta penduduk, menghasilkan menjadi keliru nomor satu wilayah demokrasi terbesar di dunia. Mekanisme politik dalam Bangsa Indonesia populer dengan keberagamannya, menyambut berlimpah partai politik yang ikut serta dalam pemilu apa diselenggarakan masing-masing lima tahun satu kali.

Libya

Setelah era Gaddafi, Libya menghadapi tantangan di dalam membentuk stabilitas politik. Struktur politik wilayah ini sering waktu berubah karena konflik internal. Libya kini dipecah beralih dua pemerintahan lain; keliru satunya dalam Timur siapa dipimpin dari Tentara Nasional Libya dalam di bawah komando Khalifa Haftar dan pemerintahan pada Barat apa diketahui dari PBB. Kondisi ini menimbulkan challenge luas bagi pembangunan demokrasi pada Libya.

Aspek Ekonomi: Pertimbangan Pertumbuhan serta Kebendaan Alam

Ekonomi Indonesia

Indonesia adalah salah nomor satu ekonomi terbesar di Asia Tenggara bersama PDB apa mencapai $1.04 triliun pada tahun 2020. Bangsa ini mendapatkan keuntungan besar dari harta alamnya yang berlimpah seperti minyak, gas alam, timah, tembaga, dan emas. Sektor pertanian juga ajeg berubah tulang punggung ekonomi dengan padi, kelapa sawit, dan juga karet menjadi komoditas pokok. Negara Indonesia pula lagi berkembang rapid internal sektor manufaktur serta digital.

Ekonomi Libya

Sumber penting pendapatan ekonomi Libya merupakan asal sektor minyak dan juga gas, yang menyumbang sekitar 60% PDB serta 97% ekspor. Walaupun berkecukupan akan asal daya minyak, konflik berkelanjutan sudah menghambat kapasitas penuh ekonomi Libya. Penyelenggaraan ekonomi sudah restriksi pada penjualan minyak, dengan some investasi dalam pembangunan infrastruktur maupun diversifikasi ekonomi.

Kesimpulan: Bangsa Indonesia vs Libya

Perbandingan di tengah Negara Indonesia dan juga Libya mengungkapkan kontras yang berarti dalam sudut politik dan ekonomi. Negara Indonesia, bersama sistem demokratisnya, telah menunjukkan pergerakan siapa berkelanjutan walaupun still menghadapi challenge internal perkara korupsi dan ketidaksetaraan sosial. Selama Libya still berjuang meraih kestabilan politik siapa berimbas atas seluruh pertumbuhan ekonominya.

Indonesia dan juga Libya, nomor dua negara bersama kemungkinan besar akan tetapi bersama challenge dan jalur pembangunan siapa berbeda, memberikan insight penting perihal bagaimana keadaan politik bisa mempengaruhi keberhasilan ekonomi satu wilayah. Pembangunan apa berkelanjutan serta stabil politik still berubah kunci utama bagi nomor dua bangsa guna meningkatkan keadaan ekonominya dalam masa yang bakal datang.

Dalam membahas “Bangsa Indonesia vs Libya”, kami tidak sekedar menyaksikan perbedaan, melainkan pula mengerti faktor-faktor yang menyusun kedua negara ini oleh karena itu sanggup menghadiahkan pelajaran penting bagi countries lain siapa mempunyai keadaan serupa. Meski dipisahkan dengan jarak dan juga variasi kultural, studi komparatif ini membantu memperkaya pemahaman kami mengenai gerakan global saat ini.